Cheng Luo - MINI-SEQUENCE TRANSFORMER (MST)

Transformers have revolutionized natural language processing and continue to push the boundaries of what's possible in AI. However, as these models grow in size and capability, they face increasing challenges in handling long sequences during training. The memory demands for processing extended contexts can quickly overwhelm even high-end GPUs, limiting our ability to train on lengthy inputs that are critical for tasks like long-form document understanding, extended conversations, and multimodal reasoning.

Understanding the Transformer Architecture

To grasp where these challenges come from, let's simplify the architecture of a transformer model like Llama. Essentially, Llama is built from a stack of identical units called transformer blocks. By focusing on a single transformer block, we can understand the computations involved throughout the entire model.

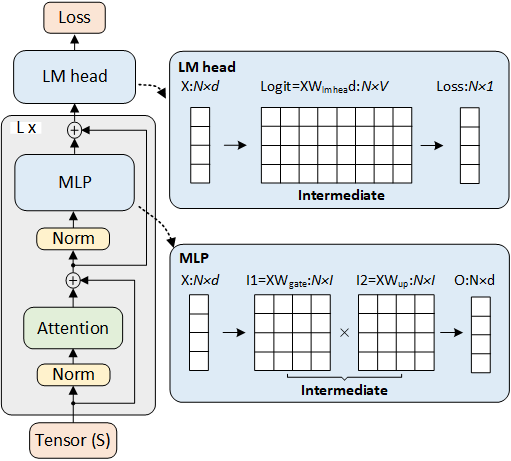
The diagram above illustrates the overall architecture of llama and a transformer block. A transformer block consists of three main components:.

Self-Attention: This mechanism allows the model to weigh the importance of different tokens (words or subwords) in the input sequence when processing each token.
Multilayer Perceptron (MLP): A feedforward neural network that processes the output from the self-attention layer to capture complex patterns.
Language Modeling Head (LM-Head): A final linear layer that maps the processed information to a probability distribution over the vocabulary, helping predict the next token in a sequence.

For simplicity, we'll ignore some additional components like Layer Normalization, masking, dropout, and residual connections. Instead, we'll focus on the tensor shapes and sizes involved in the computations, which are crucial for understanding the model's memory usage and computational requirements.

Key Parameters of Llama Models

Different versions of Llama have varying sizes and capabilities. Here's a table summarizing some key parameters:

Feature	LLAMA2-7B	LLAMA3-8B	LLAMA3.1-8B
Layers	32	32	32
Hidden Size (`d`)	4096	4096	4096
Sequence Length (`s`)	4096	8192	131072
MLP Intermediate Size (`I`)	11008	14336	14336
Vocabulary Size (`V`)	32000	128256	128256

Observations:

Increased MLP Size: LLAMA3 models have a larger MLP intermediate size (I), increasing from 11,008 to 14,336. This allows the model to capture more complex patterns but increases computational demands.
Larger Vocabulary: The vocabulary size (V) has grown from 32,000 to 128,256, accommodating more words and subwords but also increasing the size of certain tensors.
Longer Sequences: LLAMA3.1 supports much longer sequences (s), up to 131,072 tokens. While this enables the model to process longer inputs, it significantly increases the computational load.

Tensor Shapes and Their Impact on Computation

Understanding the shapes of tensors (multi-dimensional arrays) in the model helps us identify where computational challenges arise.

Scalars and Input Shapes

Batch Size (b): Number of sequences processed in parallel (e.g., b = 1).
Sequence Length (s): Length of each input sequence (e.g., s = 8192 or 131072).
Hidden Size (d): Size of the hidden state vector in the model (e.g., d = 4096).
MLP Intermediate Size (I): Size of the intermediate vector in the MLP (e.g., I = 14336).
Vocabulary Size (V): Number of unique tokens the model can predict (e.g., V = 128256).

Key Tensors in the Transformer Block

Input Tensor (X): Shape (b, s, d)
- Represents the input embeddings for the sequence.
Self-Attention Computations:
- Queries (Q): Result of X projected by W_Q, shape (b, s, d)
- Keys (K): Result of X projected by W_K, shape (b, s, d)
- Values (V): Result of X projected by W_V, shape (b, s, d)
MLP Computations:
- Intermediate Tensors:
  - XW_up: Shape (b, s, I)
  - XW_gate: Shape (b, s, I)
- These are combined and transformed back to shape (b, s, d).
LM-Head Output:
- Logits (logit): Result of X projected by W_LM-HEAD, shape (b, s, V)

Challenges with Large Tensors

Memory Usage:
- The LM-Head output tensor has a shape of (b, s, V). With large s and V, this tensor becomes enormous.
  - For s = 131072 and V = 128256, the tensor requires over 33 GB of memory just to store the logits.
- The MLP intermediate tensors (XW_up and XW_gate) have shapes of (b, s, I), also consuming significant memory.
  - For s = 131072 and I = 14336, the tensor requires over 7.5G GB of memory just to store the intermediate.
Comparison:
- Other tensors like X, Q, K, and V have shapes (b, s, d). With d being smaller than V and sometimes I, these tensors are relatively smaller in size of 1GB.
- In the early stages of transformer development, the self-attention mechanism was considered the main memory bottleneck during training. Specifically, the QK^K resulting in a tensor of shape (b, s, s, head), where h is the number of attention heads. or example, with a sequence length of 131072 tokens and 16 heads, the attention tensor would have dimensions (1, 131072 , 131072 , 16), which requires 550G GB.
- FlashAttention optimize it the attention, make it small as Q with shapes (b, s, d) in size of 1GB. That open the door of optimizing the other large tensors

Mini-Sequence Processing to Optimize Memory Usage

To handle the computational challenges posed by large tensor sizes, especially with long sequences and large vocabularies, we can adopt the following strategy:

Partitioning Input Sequences

Divide the Sequence: Split the input sequence into M smaller chunks or mini-sequences of length s/M.
Process Mini-Sequences Iteratively:
- Instead of processing the entire sequence at once, we process each mini-sequence one after the other.
Reduced Tensor Sizes:
- MLP Intermediate Tensors:
  - Original size: (b, s, I)
  - Reduced size: (b, s/M, I)
- LM-Head Output Tensors:
  - Original size: (b, s, V)
  - Reduced size: (b, s/M, V)
Memory Reduction:
- By choosing a suitable M, we can reduce the memory required for these tensors by a factor of M.
- With a large enough M, the intermediate memory usage becomes manageable.

Thankfully, some smart people have already discovered the approach similarity as mini-batch training, which is deployed as gradient accumulation on multiple library. We can try implementing this technique on sequence level and work out the necessary details.

Congratulations! We’ve essentially know the key idea of Mini-Sequence Transformers [NeurIPS’24] paper. Additionally, I recommend checking out this awesome repo of Mini-Sequence Transformers.

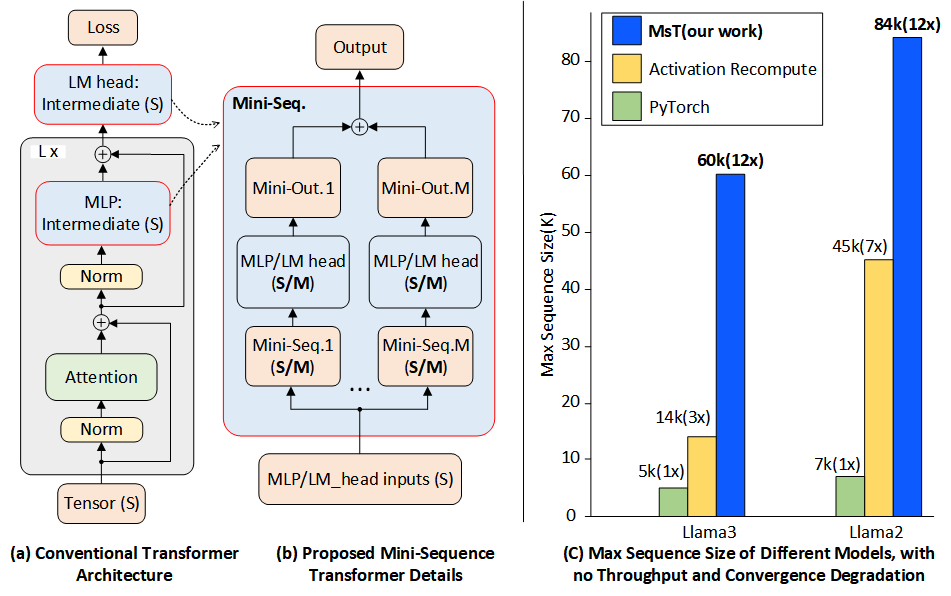
Sequence Extension

Let's dive into the details of how optimized intermediate memory usage enables training on long sequences.

Theorem: Sequence Extension

Mini-Sequence Transformers (MST) can reduce intermediate memory usage by a factor of M. Working together with gradient checkpoint The total memory occupation becomes:

$$\text{Memory} = W_{\text{mem}} + S \times \left( \dfrac{I_{\text{mem}}}{M} + \sqrt{L} \times A_{\text{mem}} \right),$$

where:

W_mem is the memory occupied by the model weights.
S is the sequence length.
I_mem is the memory per token for intermediate computations in the MLP and LM-Head.
L is the number of layers.
A_mem is the memory per token per layer for attention.

For a GPU with maximum memory M_max, the maximum sequence length is:

$$S_{\text{max}} = \dfrac{M_{\text{max}} - W_{\text{mem}}}{\dfrac{I_{\text{mem}}}{M} + \sqrt{L} \times A_{\text{mem}}},$$

Going a step further, when we combine it with CPU offload technology:

$$S_{\text{max}} = \dfrac{M_{\text{max}} - W_{\text{mem}}}{\dfrac{I_{\text{mem}}}{M} + A_{\text{mem}}},$$

which is significantly longer than the standard implementation, where the maximum sequence length is:

$$S_{\text{max}} = \dfrac{M_{\text{max}} - W_{\text{mem}}}{I_{\text{mem}} + L \times A_{\text{mem}}}.$$

This demonstrates that by reducing the intermediate memory with MST, we can train models with much longer sequences within the same memory constraints.

Example Implementation

We have developed methods and libraries to facilitate this approach. By installling the mini-sequence wrapper pip install -U https://github.com/wdlctc/mini-s, you can efficiently train large transformer models with long sequences.


from minis.mini_sequence import minisequence
model = minisequence(model)

Key Takeaway

Efficient Long-Sequence Training: By partitioning sequences, models like LLAMA3-8B can be trained with sequence lengths up to 60k tokens on a single high-end GPU.
Memory Optimization: Reduces the memory required for large intermediate tensors, addressing one of the main bottlenecks in training large models.
Maintains Throughput: Despite processing sequences in parts, the overall training speed remains comparable to standard implementations.
Easy Integration: The approach can be integrated into existing training frameworks with minimal code changes, making it accessible for practitioners.
General Applicability: Supports various training methods and is not limited to specific model architectures or configurations.

Conclusion

Understanding the tensor shapes and sizes in transformer models is crucial for identifying computational challenges and optimizing training. By focusing on how the dimensions of these tensors impact memory usage, especially with large sequence lengths and vocabulary sizes, we can develop strategies to make training more efficient.

Partitioning input sequences and processing them as mini-sequences is an effective way to reduce memory usage without sacrificing performance. This approach enables the training of large transformer models on long sequences using available hardware, paving the way for advancements in natural language understanding and generation tasks.

Note: For those interested in implementing these techniques, tools like the Mini-Sequence Transformers library are available and can be integrated into your projects to facilitate efficient training on long sequences.

Optimizing Intermediate Values in Transformers